Angles in a 3D ball of hexagons and squares (truncated octahedron)












1












$begingroup$


Trying to make a 3D-model of a "ball" made up of squares and hexagons:





Given a square and four hexagons connecting to the square sides, what is the angle required between the square plane and the hexagon planes to make two sides of each hexagon connect with the sides of the two neighbouring hexagons?






angle solid-geometry







share|cite|improve this question











$endgroup$








  • 1




    $begingroup$
    The dihedral angle of a cuboctahedron is $theta= cos^{-1} (frac{-1}{sqrt{3}}) simeq 125.26$. en.wikipedia.org/wiki/Cuboctahedron
    $endgroup$
    – Donald Splutterwit
    Apr 29 '17 at 12:52










  • $begingroup$
    @Donald Splutterwit Sorry but it's not a cuboctahedron (en.wikipedia.org/wiki/Cuboctahedron) but a truncated tetrahedron.
    $endgroup$
    – Jean Marie
    Apr 29 '17 at 12:54








  • 1




    $begingroup$
    @JeanMarie Lets try truncated Octahedron en.wikipedia.org/wiki/Truncated_octahedron ... & amusingly the dihedral is the same as I previously stated $ddot smile$
    $endgroup$
    – Donald Splutterwit
    Apr 29 '17 at 13:12






  • 1




    $begingroup$
    I agree, it is a truncated Octahedron.
    $endgroup$
    – Jean Marie
    Apr 29 '17 at 13:22






  • 1




    $begingroup$
    The angle between the Hexagonal faces is $phi= cos^{-1} (frac{-1}{3}) simeq 109.47$
    $endgroup$
    – Donald Splutterwit
    Apr 29 '17 at 13:23
















1












$begingroup$


Trying to make a 3D-model of a "ball" made up of squares and hexagons:





Given a square and four hexagons connecting to the square sides, what is the angle required between the square plane and the hexagon planes to make two sides of each hexagon connect with the sides of the two neighbouring hexagons?






angle solid-geometry







share|cite|improve this question











$endgroup$








  • 1




    $begingroup$
    The dihedral angle of a cuboctahedron is $theta= cos^{-1} (frac{-1}{sqrt{3}}) simeq 125.26$. en.wikipedia.org/wiki/Cuboctahedron
    $endgroup$
    – Donald Splutterwit
    Apr 29 '17 at 12:52










  • $begingroup$
    @Donald Splutterwit Sorry but it's not a cuboctahedron (en.wikipedia.org/wiki/Cuboctahedron) but a truncated tetrahedron.
    $endgroup$
    – Jean Marie
    Apr 29 '17 at 12:54








  • 1




    $begingroup$
    @JeanMarie Lets try truncated Octahedron en.wikipedia.org/wiki/Truncated_octahedron ... & amusingly the dihedral is the same as I previously stated $ddot smile$
    $endgroup$
    – Donald Splutterwit
    Apr 29 '17 at 13:12






  • 1




    $begingroup$
    I agree, it is a truncated Octahedron.
    $endgroup$
    – Jean Marie
    Apr 29 '17 at 13:22






  • 1




    $begingroup$
    The angle between the Hexagonal faces is $phi= cos^{-1} (frac{-1}{3}) simeq 109.47$
    $endgroup$
    – Donald Splutterwit
    Apr 29 '17 at 13:23














1












1








1





$begingroup$


Trying to make a 3D-model of a "ball" made up of squares and hexagons:





Given a square and four hexagons connecting to the square sides, what is the angle required between the square plane and the hexagon planes to make two sides of each hexagon connect with the sides of the two neighbouring hexagons?






angle solid-geometry







share|cite|improve this question











$endgroup$




Trying to make a 3D-model of a "ball" made up of squares and hexagons:





Given a square and four hexagons connecting to the square sides, what is the angle required between the square plane and the hexagon planes to make two sides of each hexagon connect with the sides of the two neighbouring hexagons?






angle solid-geometry




angle solid-geometry






share|cite|improve this question















share|cite|improve this question













share|cite|improve this question




share|cite|improve this question








edited May 19 '17 at 10:07









grg

1,0431812




1,0431812










asked Apr 29 '17 at 12:39









DHaDHa

1084




1084








  • 1




    $begingroup$
    The dihedral angle of a cuboctahedron is $theta= cos^{-1} (frac{-1}{sqrt{3}}) simeq 125.26$. en.wikipedia.org/wiki/Cuboctahedron
    $endgroup$
    – Donald Splutterwit
    Apr 29 '17 at 12:52










  • $begingroup$
    @Donald Splutterwit Sorry but it's not a cuboctahedron (en.wikipedia.org/wiki/Cuboctahedron) but a truncated tetrahedron.
    $endgroup$
    – Jean Marie
    Apr 29 '17 at 12:54








  • 1




    $begingroup$
    @JeanMarie Lets try truncated Octahedron en.wikipedia.org/wiki/Truncated_octahedron ... & amusingly the dihedral is the same as I previously stated $ddot smile$
    $endgroup$
    – Donald Splutterwit
    Apr 29 '17 at 13:12






  • 1




    $begingroup$
    I agree, it is a truncated Octahedron.
    $endgroup$
    – Jean Marie
    Apr 29 '17 at 13:22






  • 1




    $begingroup$
    The angle between the Hexagonal faces is $phi= cos^{-1} (frac{-1}{3}) simeq 109.47$
    $endgroup$
    – Donald Splutterwit
    Apr 29 '17 at 13:23














  • 1




    $begingroup$
    The dihedral angle of a cuboctahedron is $theta= cos^{-1} (frac{-1}{sqrt{3}}) simeq 125.26$. en.wikipedia.org/wiki/Cuboctahedron
    $endgroup$
    – Donald Splutterwit
    Apr 29 '17 at 12:52










  • $begingroup$
    @Donald Splutterwit Sorry but it's not a cuboctahedron (en.wikipedia.org/wiki/Cuboctahedron) but a truncated tetrahedron.
    $endgroup$
    – Jean Marie
    Apr 29 '17 at 12:54








  • 1




    $begingroup$
    @JeanMarie Lets try truncated Octahedron en.wikipedia.org/wiki/Truncated_octahedron ... & amusingly the dihedral is the same as I previously stated $ddot smile$
    $endgroup$
    – Donald Splutterwit
    Apr 29 '17 at 13:12






  • 1




    $begingroup$
    I agree, it is a truncated Octahedron.
    $endgroup$
    – Jean Marie
    Apr 29 '17 at 13:22






  • 1




    $begingroup$
    The angle between the Hexagonal faces is $phi= cos^{-1} (frac{-1}{3}) simeq 109.47$
    $endgroup$
    – Donald Splutterwit
    Apr 29 '17 at 13:23








1




1




$begingroup$
The dihedral angle of a cuboctahedron is $theta= cos^{-1} (frac{-1}{sqrt{3}}) simeq 125.26$. en.wikipedia.org/wiki/Cuboctahedron
$endgroup$
– Donald Splutterwit
Apr 29 '17 at 12:52




$begingroup$
The dihedral angle of a cuboctahedron is $theta= cos^{-1} (frac{-1}{sqrt{3}}) simeq 125.26$. en.wikipedia.org/wiki/Cuboctahedron
$endgroup$
– Donald Splutterwit
Apr 29 '17 at 12:52












$begingroup$
@Donald Splutterwit Sorry but it's not a cuboctahedron (en.wikipedia.org/wiki/Cuboctahedron) but a truncated tetrahedron.
$endgroup$
– Jean Marie
Apr 29 '17 at 12:54






$begingroup$
@Donald Splutterwit Sorry but it's not a cuboctahedron (en.wikipedia.org/wiki/Cuboctahedron) but a truncated tetrahedron.
$endgroup$
– Jean Marie
Apr 29 '17 at 12:54






1




1




$begingroup$
@JeanMarie Lets try truncated Octahedron en.wikipedia.org/wiki/Truncated_octahedron ... & amusingly the dihedral is the same as I previously stated $ddot smile$
$endgroup$
– Donald Splutterwit
Apr 29 '17 at 13:12




$begingroup$
@JeanMarie Lets try truncated Octahedron en.wikipedia.org/wiki/Truncated_octahedron ... & amusingly the dihedral is the same as I previously stated $ddot smile$
$endgroup$
– Donald Splutterwit
Apr 29 '17 at 13:12




1




1




$begingroup$
I agree, it is a truncated Octahedron.
$endgroup$
– Jean Marie
Apr 29 '17 at 13:22




$begingroup$
I agree, it is a truncated Octahedron.
$endgroup$
– Jean Marie
Apr 29 '17 at 13:22




1




1




$begingroup$
The angle between the Hexagonal faces is $phi= cos^{-1} (frac{-1}{3}) simeq 109.47$
$endgroup$
– Donald Splutterwit
Apr 29 '17 at 13:23




$begingroup$
The angle between the Hexagonal faces is $phi= cos^{-1} (frac{-1}{3}) simeq 109.47$
$endgroup$
– Donald Splutterwit
Apr 29 '17 at 13:23










1 Answer
1






active

oldest

votes


















1












$begingroup$

As already stated in the comment, you're looking at part of a truncated octahedron





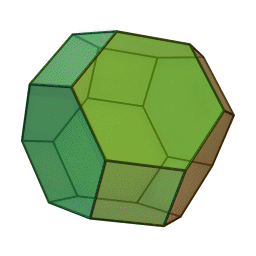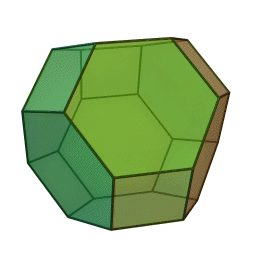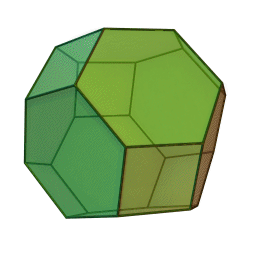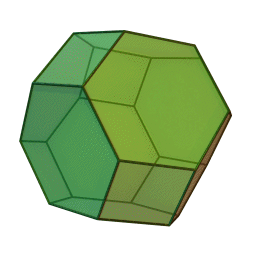
The angles between the faces are stated as well:




4-6: arccos(−1/√3) = 125°15′51″

6-6: arccos(−1/3) = 109°28′16″




If you want to check them yourself or get e.g. edge angles, note that the truncated octahedron is a permutohedron: It's coordinates are all permutations of $(1,2,3,4)$, or if projected to 3D all variations of $(0,pm1,pm2)$ (note this gives you edges of length $sqrt2$).






share|cite|improve this answer











$endgroup$













    Your Answer





    StackExchange.ifUsing("editor", function () {
    return StackExchange.using("mathjaxEditing", function () {
    StackExchange.MarkdownEditor.creationCallbacks.add(function (editor, postfix) {
    StackExchange.mathjaxEditing.prepareWmdForMathJax(editor, postfix, [["$", "$"], ["\\(","\\)"]]);
    });
    });
    }, "mathjax-editing");

    StackExchange.ready(function() {
    var channelOptions = {
    tags: "".split(" "),
    id: "69"
    };
    initTagRenderer("".split(" "), "".split(" "), channelOptions);

    StackExchange.using("externalEditor", function() {
    // Have to fire editor after snippets, if snippets enabled
    if (StackExchange.settings.snippets.snippetsEnabled) {
    StackExchange.using("snippets", function() {
    createEditor();
    });
    }
    else {
    createEditor();
    }
    });

    function createEditor() {
    StackExchange.prepareEditor({
    heartbeatType: 'answer',
    autoActivateHeartbeat: false,
    convertImagesToLinks: true,
    noModals: true,
    showLowRepImageUploadWarning: true,
    reputationToPostImages: 10,
    bindNavPrevention: true,
    postfix: "",
    imageUploader: {
    brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
    contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
    allowUrls: true
    },
    noCode: true, onDemand: true,
    discardSelector: ".discard-answer"
    ,immediatelyShowMarkdownHelp:true
    });


    }
    });














    draft saved

    draft discarded


















    StackExchange.ready(
    function () {
    StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f2257534%2fangles-in-a-3d-ball-of-hexagons-and-squares-truncated-octahedron%23new-answer', 'question_page');
    }
    );

    Post as a guest















    Required, but never shown

























    1 Answer
    1






    active

    oldest

    votes








    1 Answer
    1






    active

    oldest

    votes









    active

    oldest

    votes






    active

    oldest

    votes









    1












    $begingroup$

    As already stated in the comment, you're looking at part of a truncated octahedron





    The angles between the faces are stated as well:




    4-6: arccos(−1/√3) = 125°15′51″

    6-6: arccos(−1/3) = 109°28′16″




    If you want to check them yourself or get e.g. edge angles, note that the truncated octahedron is a permutohedron: It's coordinates are all permutations of $(1,2,3,4)$, or if projected to 3D all variations of $(0,pm1,pm2)$ (note this gives you edges of length $sqrt2$).






    share|cite|improve this answer











    $endgroup$


















      1












      $begingroup$

      As already stated in the comment, you're looking at part of a truncated octahedron





      The angles between the faces are stated as well:




      4-6: arccos(−1/√3) = 125°15′51″

      6-6: arccos(−1/3) = 109°28′16″




      If you want to check them yourself or get e.g. edge angles, note that the truncated octahedron is a permutohedron: It's coordinates are all permutations of $(1,2,3,4)$, or if projected to 3D all variations of $(0,pm1,pm2)$ (note this gives you edges of length $sqrt2$).






      share|cite|improve this answer











      $endgroup$
















        1












        1








        1





        $begingroup$

        As already stated in the comment, you're looking at part of a truncated octahedron





        The angles between the faces are stated as well:




        4-6: arccos(−1/√3) = 125°15′51″

        6-6: arccos(−1/3) = 109°28′16″




        If you want to check them yourself or get e.g. edge angles, note that the truncated octahedron is a permutohedron: It's coordinates are all permutations of $(1,2,3,4)$, or if projected to 3D all variations of $(0,pm1,pm2)$ (note this gives you edges of length $sqrt2$).






        share|cite|improve this answer











        $endgroup$



        As already stated in the comment, you're looking at part of a truncated octahedron





        The angles between the faces are stated as well:




        4-6: arccos(−1/√3) = 125°15′51″

        6-6: arccos(−1/3) = 109°28′16″




        If you want to check them yourself or get e.g. edge angles, note that the truncated octahedron is a permutohedron: It's coordinates are all permutations of $(1,2,3,4)$, or if projected to 3D all variations of $(0,pm1,pm2)$ (note this gives you edges of length $sqrt2$).







        share|cite|improve this answer














        share|cite|improve this answer



        share|cite|improve this answer








        edited Dec 27 '18 at 20:03

























        answered Dec 9 '18 at 18:33









        Tobias KienzlerTobias Kienzler

        3,4602662




        3,4602662






























            draft saved

            draft discarded




















































            Thanks for contributing an answer to Mathematics Stack Exchange!


            • Please be sure to answer the question. Provide details and share your research!

            But avoid …



            • Asking for help, clarification, or responding to other answers.

            • Making statements based on opinion; back them up with references or personal experience.


            Use MathJax to format equations. MathJax reference.


            To learn more, see our tips on writing great answers.




            draft saved


            draft discarded














            StackExchange.ready(
            function () {
            StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmath.stackexchange.com%2fquestions%2f2257534%2fangles-in-a-3d-ball-of-hexagons-and-squares-truncated-octahedron%23new-answer', 'question_page');
            }
            );

            Post as a guest















            Required, but never shown





















































            Required, but never shown














            Required, but never shown












            Required, but never shown







            Required, but never shown

































            Required, but never shown














            Required, but never shown












            Required, but never shown







            Required, but never shown







            -

            Popular posts from this blog

            Berounka

            Image
            Berounka.mw-parser-output .entete.map{background-image:url("//upload.wikimedia.org/wikipedia/commons/7/7a/Picto_infobox_map.png")} Caractéristiques Longueur 139  km Bassin 8 861  km 2 Bassin collecteur Elbe Débit moyen ? Cours Source Confluence de la Mže et de la Radbuza · Localisation Pilsen · Altitude 305  m · Coordonnées 49° 45′ 13″ N, 13° 23′ 24″ E Confluence Vltava · Localisation Prague · Altitude 187  m · Coordonnées 49° 59′ 43″ N, 14° 24′ 04″ E Géographie Pays traversés   République tchèque modifier   La Berounka est une rivière de la République tchèque. Elle porte le nom de Mže depuis sa source en Allemagne près de la frontière jusqu'à sa confluence avec la Radbuza à Plzeň. Elle continue ensuite sous le nom de Berounka jusqu'à sa confluence avec la Vltava, près de Prague. La rivière est une destination prisée pour les amateurs de canoë, qui appréc
            Read more

            Fiat S.p.A.

            Image
            Cet article court présente un sujet plus développé dans : Fiat et Fiat Chrysler Automobiles. Fiat S.p.A. Fiat S.p.A. ( Fabbrica Italiana Automobili Torino , acronyme FIAT) est un groupe, notamment connu comme société-mère du constructeur automobile italien, Fiat. Portail des entreprises Portail de Turin Portail de l’automobile This page is only for reference, If you need detailed information, please check here
            Read more

            Type 'String' is not a subtype of type 'int' of 'index'

            Image
            up vote 0 down vote favorite My App can authenticate successfully when debugging against the Android emulator, but if I try to authenticate using debugging against the physical device (with same OS version), an error message appears after more than one minute waiting: Exception has occurred. _TypeError (type 'String' is not a subtype of type 'int' of 'index') The error message points to the following code: if (responseJson[AuthUtils.authTokenKey] != null) { AuthUtils.insertDetails( userNameController.text, passwordController.text, responseJson); ... } else { ... }; And in the DEBUG CONSOLE I get the following: I/flutter ( 9531): Auth: SocketException: OS Error: Connection timed out, errno = 110, address = example.com, port = 3897
            Read more